LeetCode百题【回文子串】

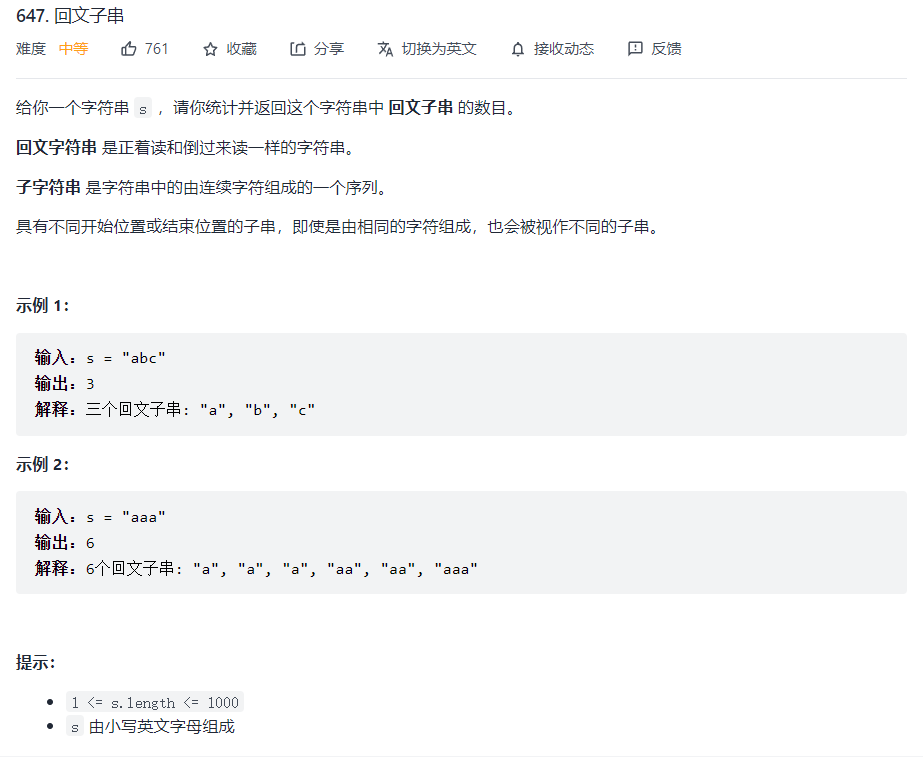
题目描述

解法一

暴力破解法

列出所有子串
判断子串是否为回文串

public class Solution {
     public static void main(String[] args) {
        String str="aaa";
         System.out.println(countSubstrings(str));
     }

    public  static int countSubstrings(String s) {
         int n=s.length();
         int cnt=0;
         String tmp;
        for (int i = 0; i < n; i++) {
            for (int j = i; j <n ; j++) {
              tmp=s.substring(i,j+1);//双重循环遍历子串 ，并将子串进行判断是否为回文串
              if(isStr(tmp)){
                  cnt++;
              }
            }
        }
        return cnt;
     }
		//判断回文串函数
     public  static boolean isStr(String str){
         int i,j;//左右指针
         j=str.length()-1;
         for(i=0;i<str.length()/2;i++){//长度为n的字符串只需要判断n/2次即可
             if(str.charAt(i)!=str.charAt(j))
                 break;
             j--;
         }
         if(i>=j)//奇数指针重合，偶数左右指针交换位置
             return true;
         else
             return false;
     }

}

时间复杂度为O(n^3)
遍历所有子串为O(n^2)判断子串为O(n)

解法二

中心扩展方法

枚举每一个可能的回文中心，然后用两个指针分别向左右两边拓展，当两个指针指向的元素相同的时候就拓展，否则停止拓展。
中心可能有一个(奇数)，也可能有两个(偶数)
长度为 n 的字符串会生成 2n-1 组回文中心
l=i/2,r=i/2+i%2

代码如下

class Solution {
    public int countSubstrings(String s) {
        int n=s.length();
        int res=0;
         for (int i = 0; i <2*n-1 ; i++) {
            int l=i/2,r=i/2+i%2;//l,r分别为左右指针
            while(l>=0&&r<n&&s.charAt(l)==s.charAt(r)){
                //l>=0&&r<n 此处是判断是否遍历完原字符串,防止越界
                //s.charAt(l)==s.charAt(r)，判断是否为回文串
                l--;
                r++;
                res++;
            }
         }
     return res;
    }
}