打家劫舍I

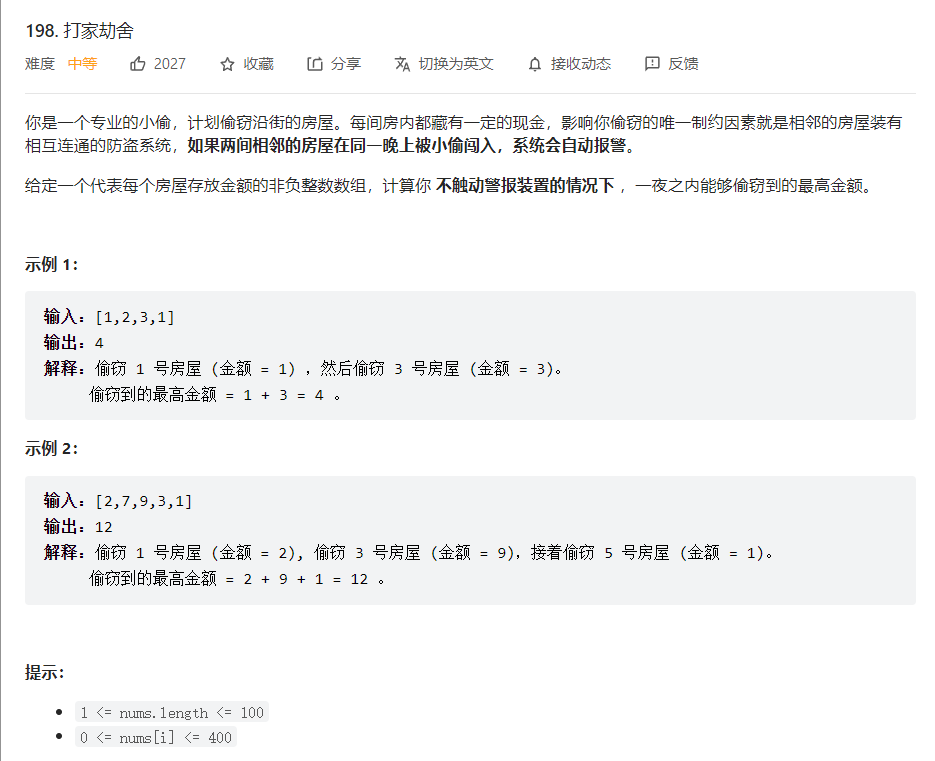
解法

  • 动态规划

    • 偷窃第i间房，所获得的金额应该为第i间房的金额+前i-2间房的最高总金额之和

    • 不偷第i间房，所获得的金额应该为前i-1间房的最高总金额之和

    • 在两个选项中选择最大的即可

    • dp[i]=max(dp[i−2]+nums[i],dp[i−1])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int rob(int[] nums) {
        if(nums.length==1){
            return  nums[0];
        }
        int dp[]=new int[nums.length];
        dp[0]=nums[0];
        dp[1]=Math.max(nums[0],nums[1]);
        for (int i = 2; i < nums.length; i++) {
            dp[i]=Math.max(dp[i-2]+nums[i],dp[i-1]);
        }
        return dp[nums.length-1];
    }
}
  • 时间复杂度：O(n)

来源：力扣（LeetCode）
链接：198. 打家劫舍 - 力扣（LeetCode） (leetcode-cn.com)

打家劫舍II

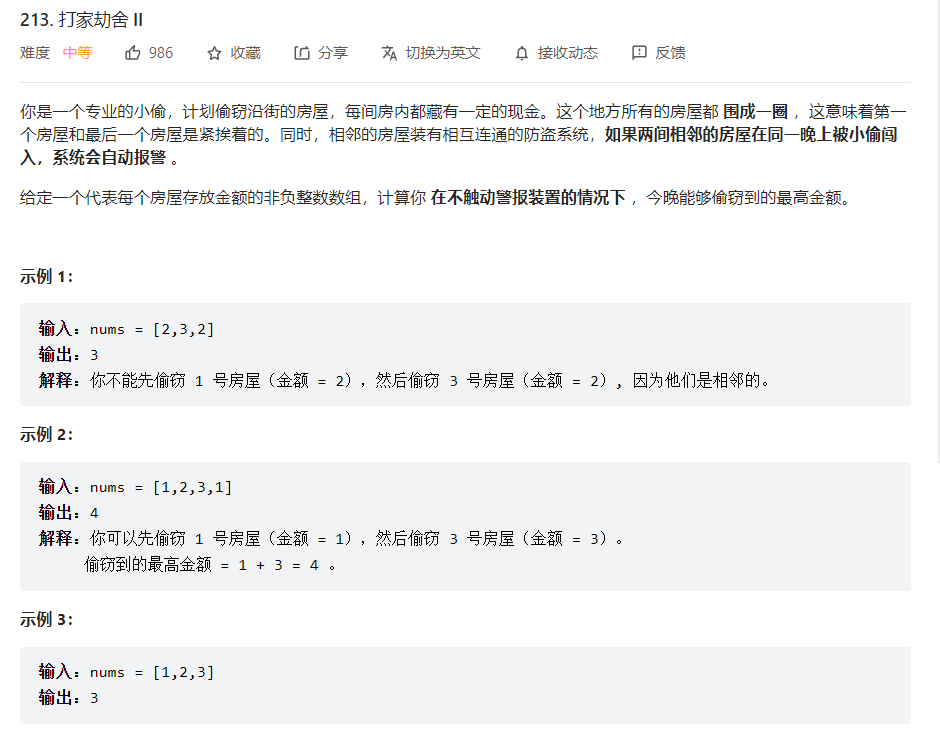
解法

  • 动态规划
  • 跟上题很相似，不同的是这次房屋围城了环
  • 解法是分两种情况变成单链采用题一的解法
    • 盗第一间房，不盗最后一间 盗窃范围：[0,n-2]
    • 不盗第一间房，盗最后一间 盗窃范围：[1,n-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int rob(int[] nums) {
        if(nums.length==1){
            return  nums[0];
        }
        else if(nums.length==2){
            return Math.max(nums[0],nums[1]);
        }
        else
            return Math.max(robRange(Arrays.copyOfRange(nums,0,nums.length-1)),robRange(Arrays.copyOfRange(nums,1,nums.length)));
//分两种情况讨论
    }
    public int robRange(int[]nums){
        int dp[]=new int[nums.length];
        dp[0]=nums[0];
        dp[1]=Math.max(nums[0],nums[1]);
        for (int i = 2; i < nums.length; i++) {
            dp[i]=Math.max(dp[i-2]+nums[i],dp[i-1]);
        }
        return dp[nums.length-1];
    }
}
  • 时间复杂度：O(n)

来源：力扣（LeetCode）
链接：213. 打家劫舍 II - 力扣（LeetCode） (leetcode-cn.com)

打家劫舍III

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 _ 在不触动警报的情况下 ，小偷能够盗取的最高金额_ 。

示例 1: 

1
2
3
输入: root = [3,2,3,null,3,null,1]
输出: 7 
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

示例 2: 

1
2
3
输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9

提示：

  • 树的节点数在 [1, 10^4] 范围内
  • 0 <= Node.val <= 10^4

解法

  • 动态规划

    • 树上的每个点都有对应的权值，每个点有两种状态（选中和不选中）

    • 我们可以计算出当前节点选中(checked)的子树的最大权值之和，和未被选中(unchecked)时的子树的最大权值

    • 如果当前节点被选中，则有转移方程

      • checked(node).val+unchecked(l)+unchecked(r)
      • 当前节点的权值之和=即当前节点的值+子节点无法被选中的权值之和

    • 如果当前节点未被选中，则有转移方程

      • max(checked(l) , unchecked(l)) + max(checked(r) , unchecked(r))
      • 当前节点的权值之和=子节点的权值之和
      • 此时因为父节点没有选择，所以子节点的状态是不固定的，我们选择贡献最大的那种情况相加
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    //1.定义选择当前节点和未选择当前节点的最大收益
    Map<TreeNode,Integer> checked=new HashMap<>();
    Map<TreeNode,Integer> unchecked=new HashMap<>();
    public int rob(TreeNode root) {
        dfs(root);
        return Math.max(checked.getOrDefault(root, 0),unchecked.getOrDefault(root, 0));
    }

    /**
     * 深度优先搜索
     * @param node
     */
    public void dfs(TreeNode node){
        //1.定义递归出口
        if (node==null){
            return;
        }
        //2.dfs
        dfs(node.left);
        dfs(node.right);
        //3.对于当前被选中的节点，maxVal=unchecked(l)+uncheck(r),因为左右孩子不能选
        checked.put(node,
                node.val+unchecked.getOrDefault(node.left, 0)
                +unchecked.getOrDefault(node.right, 0));
        //4.对于未选择的节点，它的子节点可以被选中，也可以不选，我们选择贡献最大的
        unchecked.put
                (node, Math.max(checked.getOrDefault(node.left, 0),
                                unchecked.getOrDefault(node.left, 0)) +
                        Math.max(checked.getOrDefault(node.right, 0),
                                unchecked.getOrDefault(node.right, 0)));
    }
}
  • 时间复杂度：O(n)

来源：力扣（LeetCode）
链接：337. 打家劫舍 III - 力扣（LeetCode）