LeetCode百题【最大子数组和I,II】

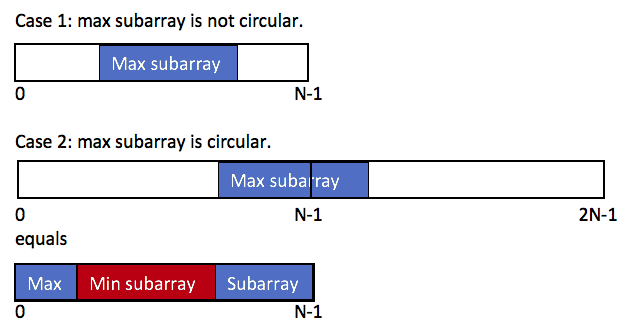
题目描述

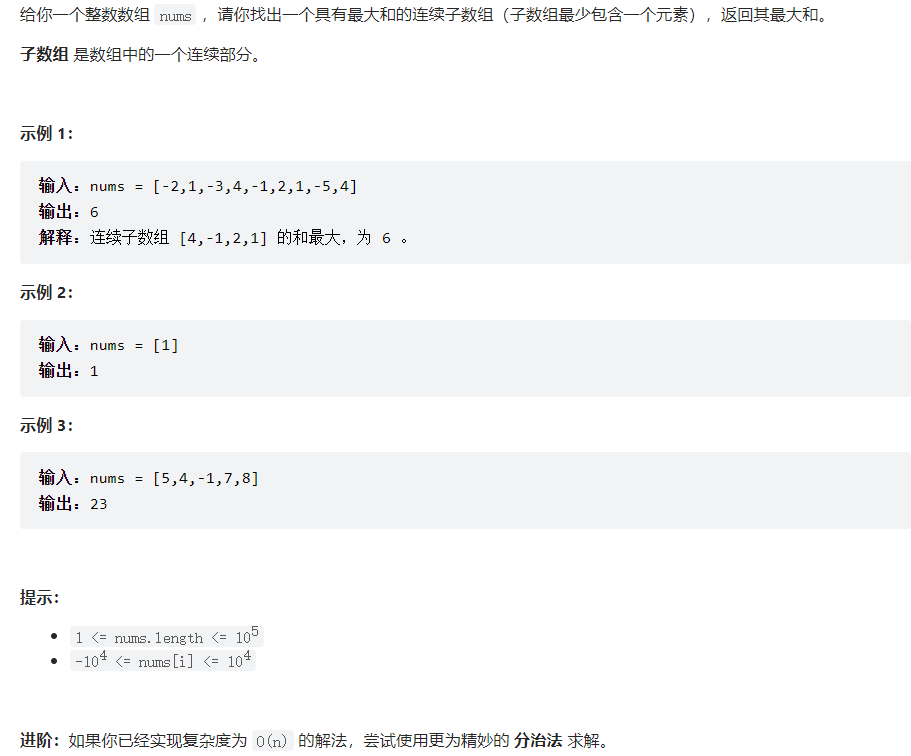
解法

动态规划
- dp[i]表示以i之前的子数组之和的最大值
- 那么dp[i+1]的值就取决于dp[i]和nums[i]的关系
- 如果dp[i-1]<0,那就另起炉灶dp[i]=nums[i]
- 如果dp[i-1]>0,那么dp[i]=dp[i-1]+num[i]

class Solution {
    public int maxSubArray(int[] nums) {
        if(nums.length==1){
            return  nums[0];
        }
        //dp为 前面n项数的和的最大值
        int []dp=new int[nums.length];
        dp[0]=nums[0];
        for (int i = 1; i < nums.length; i++) {
            /*if(dp[i-1]>0){
                dp[i]=dp[i-1]+nums[i];
            }
            else 
                dp[i]=nums[i];
            
            */
            //这里为了方便就使用下边的形势
            dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
            
        }
        int max=dp[0];
        for (int i = 1; i < dp.length; i++) {
            if(dp[i]>max){
                max=dp[i];
            }
        }
        return max;
    }
}

时间复杂度：O(n)

来源：力扣（LeetCode）
链接：53. 最大子数组和 - 力扣（LeetCode） (leetcode-cn.com)

题目描述

解法

动态规划
跟上题很相似，不同的是这次数组围成了环
解法是分两种情况
- 最大子数组不经过数组头尾，也就是跟上题一样的一般情况
- 最大子数组经过头尾
  - 这种情况下， Max=数组和-最小子数组和
同时还要考虑特殊情况，也就是全为负数，此时的最小数组和会占据整个数组之和直接用数组和-最小数组和会出错

class Solution {
    public int maxSubarraySumCircular(int[] nums) {
        if(nums.length==1){
            return  nums[0];
        }
        int []dpMax=new int[nums.length];
        int []dpMin=new int[nums.length];
        dpMax[0]=nums[0];
        dpMin[0]=nums[0];
        int arraySum=nums[0];
        
        for (int i = 1; i < nums.length; i++) {
            dpMax[i]=Math.max(dpMax[i-1]+nums[i],nums[i]);
            dpMin[i]=Math.min(dpMin[i-1]+nums[i],nums[i]);
            arraySum+=nums[i];
        }
        
        int max=dpMax[0];
        for (int i = 1; i < dpMax.length; i++) {
            if(dpMax[i]>max){
                max=dpMax[i];
            }
        }
        int min=dpMin[0];
        for (int i = 1; i < dpMin.length; i++) {
            if(dpMin[i]<min){
                min=dpMin[i];
            }
        }
        if(arraySum==min){
            return max;
        }//特殊情况
        return Math.max(max,arraySum-min);
    }
}