LeetCode百题【乘积最大子数组I,II】

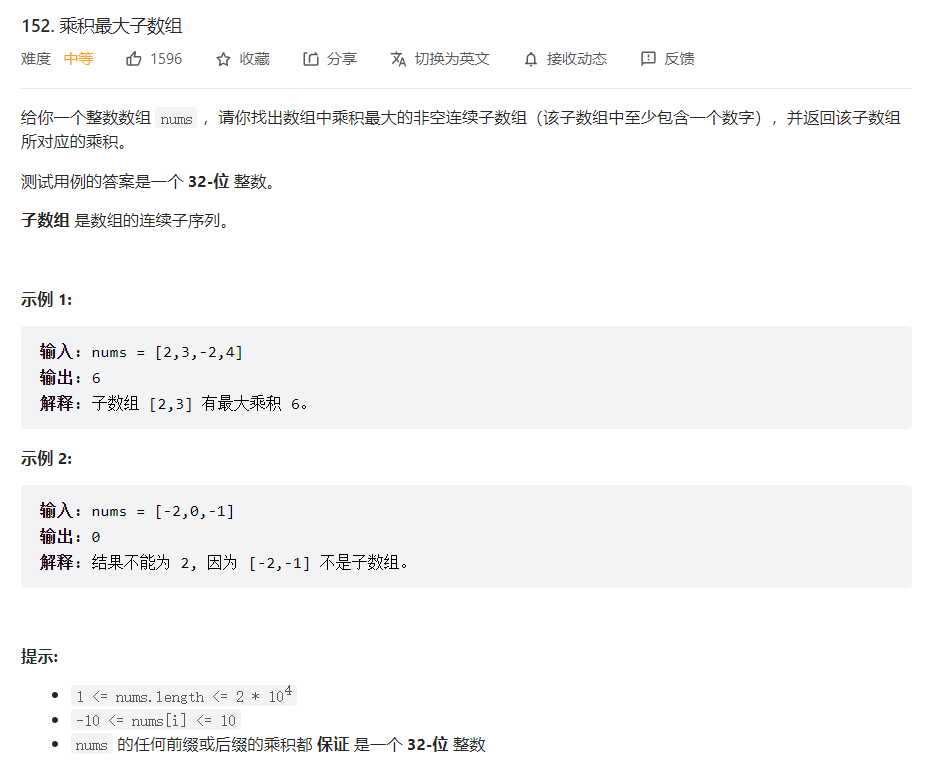
题目描述

解法

动态规划
- dp[i]为存储第i个元素结尾的乘积最大的子数值的乘积
- 很容易得到动态方程：dp[i]=dp[i-1]*nums[i]与num[i]当前值进行比较
- 问题是，当dp[i-1]与num[i]异号时，该动态方程就失效了
- 考虑当前位置如果是一个负数的话，那么我们希望以它前一个位置结尾的某个段的积也是个负数，这样就可以负负得正，并且我们希望这个积尽可能「负得更多」，即尽可能小。
- 如果当前位置是一个正数的话，我们更希望以它前一个位置结尾的某个段的积也是个正数，并且希望它尽可能地大。
- 状态转移方程为

dpMax[i]=Math.max(Math.max(dpMax[i-1]*nums[i],dpMin[i-1]*nums[i]),nums[i]);
//假设当前为正数。正数与前子序列最大积相乘---dpMax[i-1]*nums[i]
//假设当前为负数。负数与前子序列最小积相乘，负负得正---dpMin[i-1]*nums[i]
//如果存在子序列最大乘积和子序列最小乘积都为0,就东山再起，当前元素---nums[i]
//三种情况取最大值就是   第i个元素结尾的乘积最大的子数值的乘积
//dpMin类似
dpMin[i]=Math.min(Math.min(dpMin[i-1]*nums[i],dpMax[i-1]*nums[i]),nums[i]);

class Solution {
    public int maxProduct(int[] nums) {
        if(nums.length==1){
            return nums[0];
        }
        int dpMax[]=new int[nums.length];
        int dpMin[]=new int[nums.length];
        dpMax[0]=nums[0];
        dpMin[0]=nums[0];
        for (int i = 1; i < nums.length; i++) {
            dpMax[i]=Math.max(Math.max(dpMax[i-1]*nums[i],dpMin[i-1]*nums[i]),nums[i]);
            dpMin[i]=Math.min(Math.min(dpMin[i-1]*nums[i],dpMax[i-1]*nums[i]),nums[i]);
        }
        int max=dpMax[0];
        for (int i = 1; i < dpMax.length; i++) {
            if(dpMax[i]>max){
                max=dpMax[i];
            }
            
        }
        return max;
    }
}

时间复杂度：O(n)

来源：力扣（LeetCode）
链接：152. 乘积最大子数组 - 力扣（LeetCode） (leetcode-cn.com)

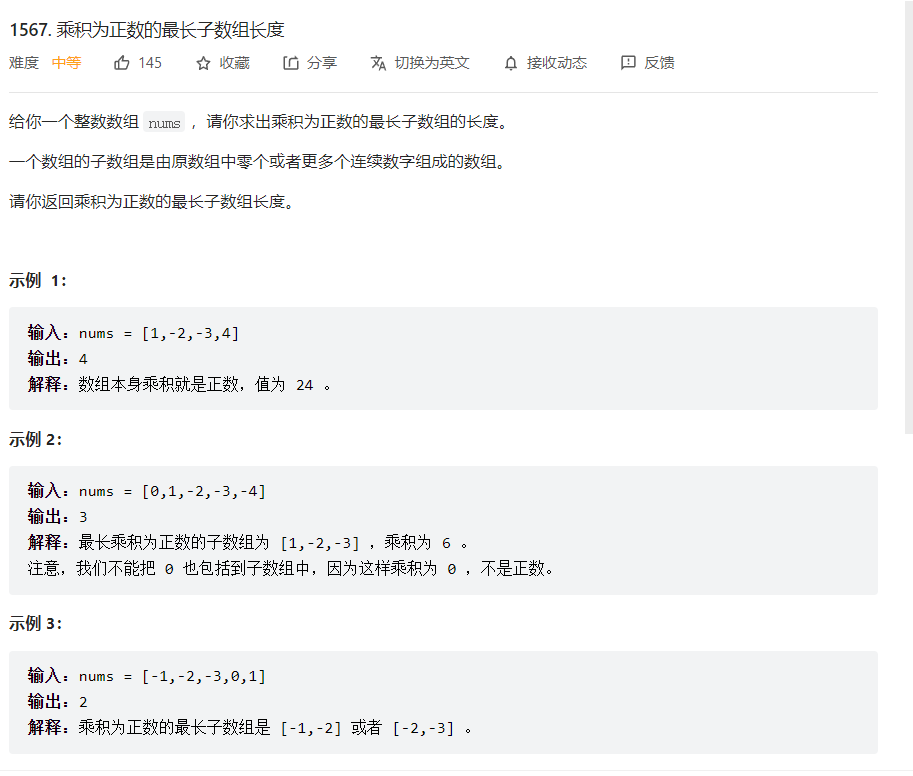
题目描述

解法

动态规划
最大乘积数组相类似，也需要维护一个最大正数和一个最大负数的长度
dp[]为数的最长子数组长度
若nums[i]>0 (dp[i]的符号不会因此改变)
正数组[i]在正数组[i-1]基础上+1 (因为正数组[i-1]是否为0不影响，因为当前的num>0)
若负数组[i-1]>0则在原来的dp[i-1]上+1，若负数组i-1为0则要置0
若nums[i]<0 (dp[i]的符号会因此改变)
- 正数组[i]在负数组[i-1]基础上+1 ,若负数组为0,则正数组置0(因为此时受到负数组[i-1]的影响，因为当前的num<0)
- 负数组[i]在正数组[i-1]基础上+1 (因为正数组[i-1]是否为0不影响，因为当前的num<0)

若num[i]=0,两个数组都要重新计数

class Solution {
    public int getMaxLen(int[] nums) {
        int dpPositive[]=new int[nums.length];
        int dpNegative[]=new int[nums.length];
        dpPositive[0]=0;
        dpNegative[0]=0;
        if(nums[0]>0)
            dpPositive[0]=1;
        else if (nums[0]<0)
            dpNegative[0]=1;
        
        for (int i = 1; i < nums.length; i++) {
            if(nums[i]>0){
                dpPositive[i]=dpPositive[i-1]+1;
                if(dpNegative[i-1]>0)
                    dpNegative[i]=dpNegative[i-1]+1;
                else
                    dpNegative[i]=0;
            }
            else if (nums[i]<0){
                if(dpNegative[i-1]>0)
                    dpPositive[i]=dpNegative[i-1]+1;
                else
                    dpPositive[i]=0;
                dpNegative[i]=dpPositive[i-1]+1;
            }else{
                dpNegative[i]=0;
                dpPositive[i]=0;
            }
        }
        int max=dpPositive[0];
        for (int i = 1; i < dpPositive.length; i++) {
            if(dpPositive[i]>max){
                max=dpPositive[i];
            }
        }
        return max;
    }
}