LeetCode百题【下一个排列】

题目描述

整数数组的一个排列就是将其所有成员以序列或线性顺序排列。

例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。

整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

给你一个整数数组 nums ，找出 nums 的下一个排列。

必须原地修改，只允许使用额外常数空间。

示例 1：

1 2	`输入：nums = [1,2,3] 输出：[1,3,2]`

示例 2：

1 2	`输入：nums = [3,2,1] 输出：[1,2,3]`

示例 3：

1 2	`输入：nums = [1,1,5] 输出：[1,5,1]`

提示：

1 <= nums.length <= 100
0 <= nums[i] <= 100

解法

两次扫描
我们需要使得新的序列相对于原来的序列变化尽可能的小
- 我们需要将一个左边的「较小数」与一个右边的「较大数」交换，以能够让当前排列变大，从而得到下一个排列。
- 同时我们要让这个「较小数」尽量靠右，而「较大数」尽可能小。
- 当交换完成后，「较大数」右边的数需要按照升序重新排列。这样可以在保证新排列大于原来排列的情况下，使变大的幅度尽可能小。
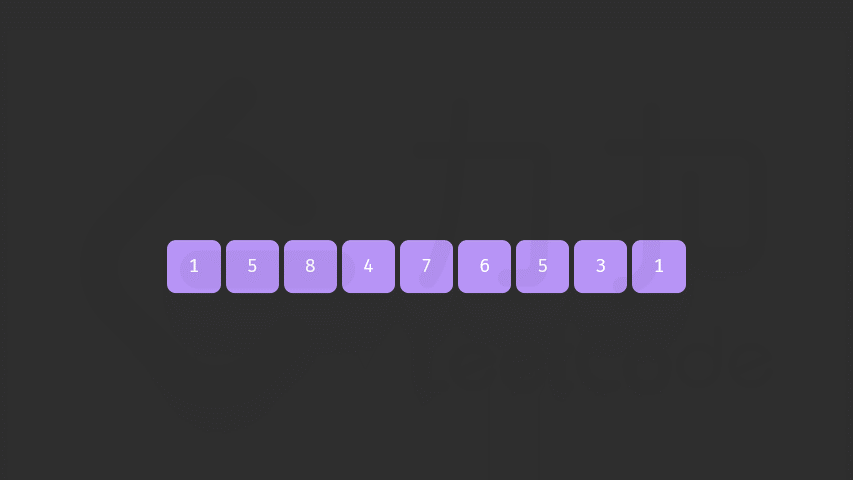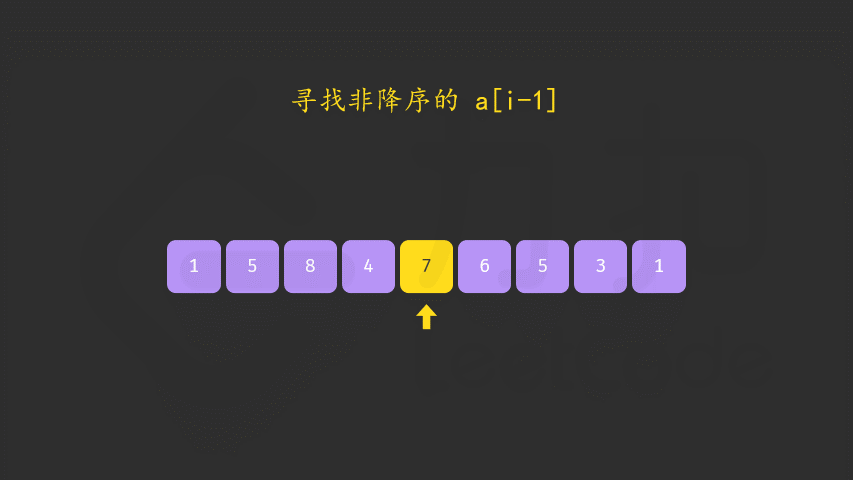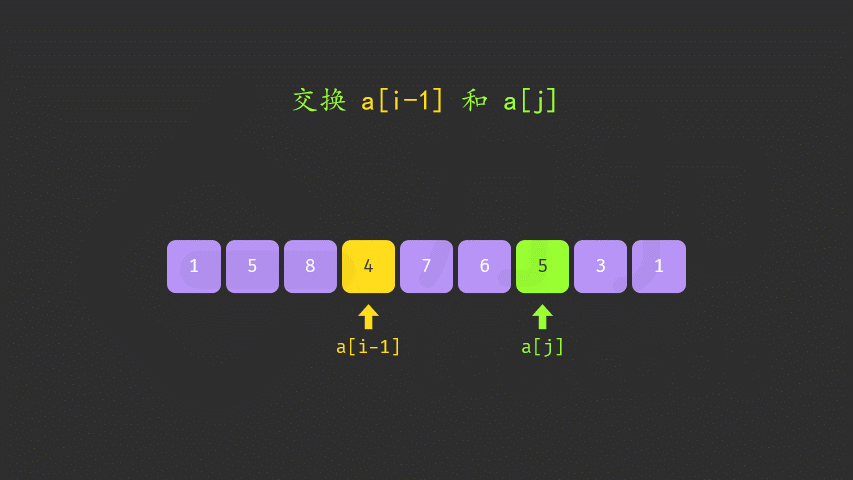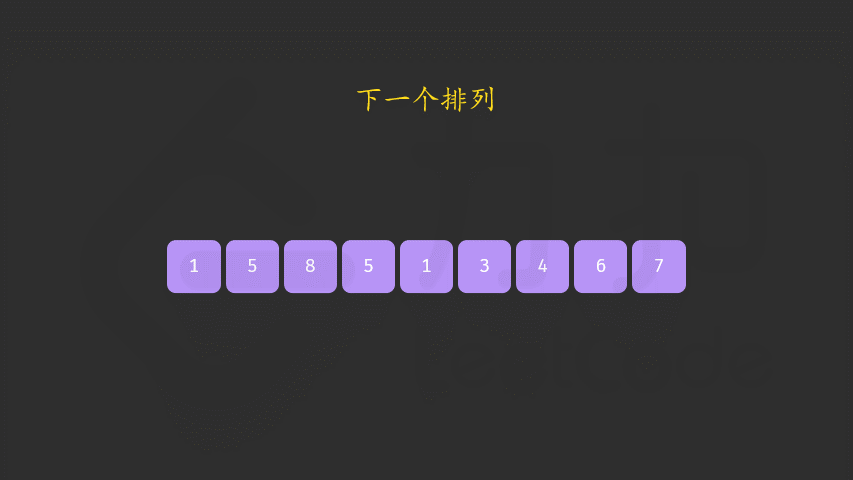
- 我们从右往左找第一个非降序排列的数作为「较小数」
  - 此时易证从i+1到末尾全为倒序排列
- 然后从右往左找第一个大于这个最小数的数作为「较大数」
- 然后交换这两个数，对i后边的数进行正序排列

class Solution {
   public void nextPermutation(int[] nums) {
        //1.寻找左边的较小值， 从用往左第一个非倒序的
        int i= nums.length-2;
        while (i>=0&&nums[i]>=nums[i+1]){
            i--;
        }
        //如果是全倒序，那下一个就是最小值
        //eg：4321 ——> 1234
        if (i>=0){
            //2.寻找右边的较大值，第一个比nums[i]大的
            int j= nums.length-1;
            while (j>=0&&nums[i]>=nums[j]){
                j--;
            }
            //3.交换
            swap(nums,i,j);
        }
        //4.排序
        Arrays.sort(nums, i+1, nums.length);
    }

    private void swap(int[] nums, int i, int j) {
        int tmp=nums[i];
        nums[i]=nums[j];
        nums[j]=tmp;
    }
}