LeetCode百题【从前序与中序遍历序列构造二叉树】

题目描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的 先序遍历 ， inorder 是同一棵树的 中序遍历 ，请构造二叉树并返回其根节点。

示例 1:

1 2	`输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]`

示例 2:

1 2	`输入: preorder = [-1], inorder = [-1] 输出: [-1]`

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

解法

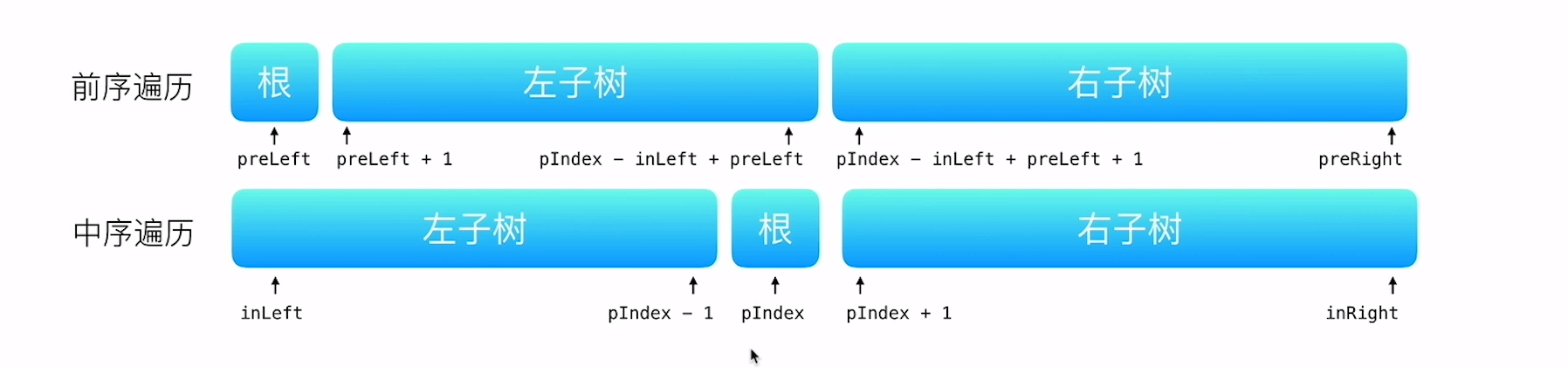
对于任意一颗树而言，前序遍历的形式总是
- [ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是
- [ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]
只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。

class Solution {

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        //1.俩数组长度
        int preLen=preorder.length;
        int inLen=inorder.length;
        //2.哈希表存储inorder中序遍历的值与下标
        Map<Integer,Integer> map=new HashMap<>();
        for (int i = 0; i < inLen; i++) {
            map.put(inorder[i],i);
        }
       return buildTree(preorder, map, 0, preLen-1, 0, inLen-1);
    }

    /**
     * 函数重载
     * @param preorder  先序遍历的数组
     * @param map       存储中序遍历的映射关系
     * @param preLeft   先序遍历子区间的最左端
     * @param preRight  先序遍历子区间的最右端
     * @param inLeft    中序遍历子区间的最左端
     * @param inRight   中序遍历子区间的最右端
     * @return
     */
    public TreeNode buildTree(int[] preorder,Map<Integer,Integer> map, int preLeft,int preRight, int inLeft,int inRight){
        //1.定义递归出口
        if (preLeft>preRight||inLeft>inRight){
            return null;
        }
        //2.创建根节点
        int rootVal=preorder[preLeft];
        TreeNode root=new TreeNode(rootVal);

        //3.获取根节点在中序遍历中的位置
        int pIndex = map.get(rootVal);

        int lengthTheInterval=pIndex-inLeft; //子树的区间长度

        //4.递归遍历左右子树
        root.left=buildTree(preorder, map, preLeft+1, preLeft+lengthTheInterval, inLeft, pIndex-1);
        root.right=buildTree(preorder, map, lengthTheInterval+preLeft+1, preRight, pIndex+1, inRight);
        return root;
    }
}