LeetCode百题【零钱兑换】

题目描述

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

1
2
3

输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

示例 2：

1 2	`输入：coins = [2], amount = 3 输出：-1`

示例 3：

1 2	`输入：coins = [1], amount = 0 输出：0`

提示：

1 <= coins.length <= 12
1 <= coins[i] <= 2^31 - 1
0 <= amount <= 10^4

解法

动态规划
- 定义dp[i]为组成金额 i 所需最少的硬币数量
- 动态转移方程为
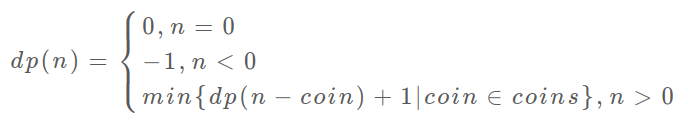
- 即我们枚举最后一枚硬币面额是coin，那么需要从dp[i-coin]这个金额的状态转移过来,再算上枚举的这枚硬币数量1的贡献
- 由于要硬币数量最少，所以dp[i]为前面能转移过来的状态的最小值加上枚举的硬币数量1 。

class Solution {

    public int coinChange(int[] coins, int amount) {
        int max=amount+1;
        int [] dp=new int[max];//数组从0-amount
        Arrays.fill(dp, max);//全部填充最大值 amount+1假设无法找零
        dp[0]=0;//初始化
        for (int i = 1; i<max; i++) {
            //遍历从1-amount更新对应的最小硬币数
            for (int j = 0; j < coins.length; j++) {
                //遍历所有面额
                if (coins[j]<=i){
                    //可以进行找零,维护最小值
                    dp[i]=Math.min(dp[i],dp[i-coins[j]]+1);
                }
            }
        }
        return dp[dp.length-1] >amount ? -1:dp[dp.length-1];
    }
}