剑指Offer【二叉搜索树的后序遍历序列】

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

示例 1：

1 2	`输入: [1,6,3,2,5] 输出: false`

示例 2：

1 2	`输入: [1,3,2,6,5] 输出: true`

提示：

数组长度 <= 1000

解法

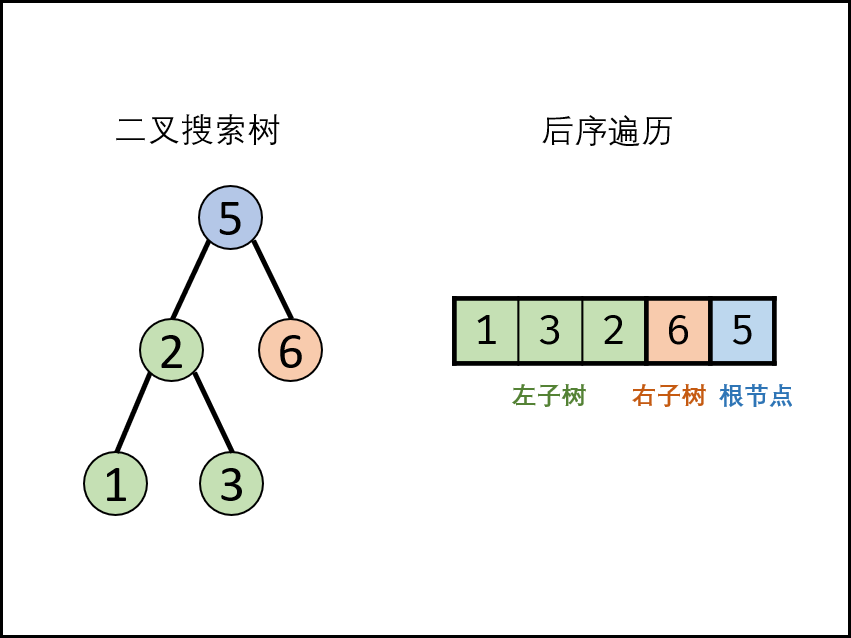
递归判断
- 后序遍历定义： [ 左子树 | 右子树 | 根节点 ] ，即遍历顺序为 “左、右、根” 。
- 二叉搜索树定义：左子树中所有节点的值 < 根节点的值；右子树中所有节点的值 > 根节点的值；其左、右子树也分别为二叉搜索树。
  - 划分左右子树:遍历后序遍历的 [i,j]区间元素，寻找第一个大于根节点的节点，索引记为m 。此时，可划分出左子树区间 [i,m−1] 、右子树区间[m,j−1]根节点索引 j。
  - 左子树区间:[i,m−1]内的所有节点都应 <postorder[j] 。而划分左右子树步骤已经保证左子树区间的正确性，因此只需要判断右子树区间即可。
  - 右子树区间:[m,j−1]内的所有节点都应 >postorder[j]。实现方式为遍历，当遇到<=postorder[j]的节点则跳出,后续则可通过 p = j判断是否为二叉搜索树。（p为遍历的指针）
  - 递归终止条件:i>=j

class Solution {

    public boolean verifyPostorder(int[] postorder) {
        return check(postorder, 0, postorder.length - 1);
    }

    /**
     * 检验二叉树的后序遍历
     *
     * @param postorder 需要遍历的数组
     * @param i         遍历的左区间
     * @param j         遍历的右区间
     * @return
     */
    public boolean check(int[] postorder, int i, int j) {
        //1.定义递归条件
        if (i >= j) {
            return true;
        }
        int point = i;
        //2.划分左右子树(寻找到第一个比根节点大的节点，以此为界)
        while (postorder[point] < postorder[j]) {
            point++;
        }
        int m = point;
        //3.右子树遍历检测
        while (postorder[point] > postorder[j]) {
            point++;
        }
        //递归判断
        return point == j && check(postorder, i, m - 1) && check(postorder, m, j - 1);

    }
}